PART I: Math Preliminaries #
String and apphabet #
language: 一个字符串组成的集合:cat, dog, ...
string: 字符 (letter) 序列,字符从 alphabet (如 \(\sum = {a, b, c, d, …, z}\)) 而来。
对一个简单的 alphabet \(\sum = {a, b}\),
- Strings: a, b, aab, ….
- Language:string 全集的任意子集;或者说 Kleene Star 的任意子集
String opeartion #
1. Concatenation #
$$ w_1 = aabb $$ $$ w_2 = bbaa $$ $$ w_1w_2 = aabbbbaa $$
2. Reverse #
$$ w = abcd $$ $$ w^R=dcba $$
3. Length #
$$w = a_1a_2a_3a_4$$ $$|w| = 4$$
Empty String #
\(\epsilon\) \(|\epsilon| = 0\) \(\epsilon aabb = aabb\),也就是说可以放在任何地方
Sub-string #
Substring: 子串 Prefix and suffix: \(w = uv\), u 是 prefix, v 是 suffix, u/v 可以是 \(\epsilon\)
Power, Kleene Star, Plus #
Power #
- \(w^n\) 是 n 个 w 拼接在一起
- \(w^0\) 必是 \(\epsilon\)
Kleene Star #
对一个简单的 alphabet \(\sum = {a, b}\) Kleene Star \(\sum^{\ast}\) 是所有用 alphabet 组成的 string 的集合,包括空集 Language 的新定义:Kleene star 的任意非空子集,包括 \({ \epsilon }\)
Plus #
\(\sum^+\) = \(\sum^{\ast}\) - \({ \epsilon }\)
Operation on Languages #
- 并,交,减

- 补 Complement: 等于 Kleene Star 减去自身

- Reverse:

- Concatenation: 有点像 笛卡尔积

- 实例:

- 实例:
- Power

- Star-Closure

- Positive-Closure

PART II: Deterministic Finite Automata #
Intro #
有限状态机的输入是一个 String, 经过有限状态机后,输出"Accept"或"Reject".
-

-

DFA 的表示 #
- 五元组表示

- \(Q\): 有限数量的状态,如 \(q_1, q_2, \ldots\)
- \(\sum\): 有限集,元素是字符,是有限机的输入
- \(\sigma\) : 转换方程,可以列表格表示
- \(q\): 当前状态
- \(a\): 字母,下一次输入
- \(q’\): 下一个状态
- \(q_0\): 起始状态, 唯一
- \(F\): final state 的集合。
转换方程有扩展版的,此时 \(\sum\) 变成了其 Kleene Star, 也就是输入多个字符,one at a time
用 DFA 定义语言 #
能够被某个状态机 \(M = (Q, \sum, \theta, q_0, F)\) 接受的 language (也就是说,language 的 string 作为输入进入 DFA 能停在 final state)被记作 $$ L(M) = {w \in \Sigma^* | \sigma^*(q_0, w) \subseteq F } $$
DFA Minimization #
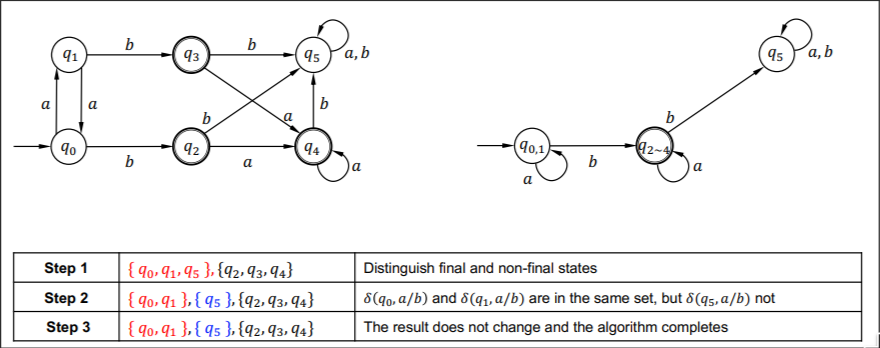
- 先把非 final state 放进一个集合,final state 放在一个集合
- 查看每个集合中的每一个状态接受某个输入后的下一个状态,如果这个集合接受相同的输入进入的下一个状态都在一个集合,就合法;否则不合法,要把不合法的状态放进新的集合。
- 重复这个操作,知道无法再细分。
这种算法的平均复杂度: $$ \Omega(n \log \log n) $$
DFA Bi-Simulation #
一种用于分析和比较两个 DFA 行为等价性的技术。Bi-Simulation 的核心思想是通过建立一种关系,使得两个 DFA 的状态在某种意义上“行为相似”,即一个 DFA 的行为可以模拟另一个 DFA 的行为,反之亦然。
在 DFA 的上下文中,Bi-Simulation 关系通常用于证明两个 DFA 是否接受相同的语言, 即,\(L (M_1) = L(M_2)\)
算法 #
等价条件 #
给一个输入字符串,让要进行比较的两个有限机共同运作,让
$$M_1 到达 finalstate$$ 和
$$M_2 到达 finalstate$$
是等价条件,则认为二者等价。
具体步骤 #
- 将两个DFA 的初始状态配成一个 state pair
- 让这个 pair 接受所有可能的输入,分别产生新的 state pair;
- 观察产生的 state pair,
- 如果满足上面提价的等价条件,则继续,否则肯定不等价;
- 将产生的新的(和之前不重复的)state pair 重复第二部,接受输入继续产生 state pair….
- 直到无法产生新的 state pair, 如果始终满足等价条件,则两个 DFA 确实等价。
概括地说,如果存在一个双模拟关系,使得两个 DFA 的初始状态相关联,并且这种关系能够扩展到所有可达状态,则这两个 DFA 被认为是等价的。
PART III: Non-deterministic Finite Automata #
Intro #
之前说过,输入确定,DFA 的每一步都是只有一种情况的,本节的状态机就有不止一种。
-

- 如上例,aa只要有一条路径能走到 final state, 就可是说是被 accepted 了。
NFA 的表示 #
-
\(\epsilon ~transition\): 不消耗任何输入也能进行的状态转换。
-

-
仍然用五元组表示,但区别:
- \(\Sigma \cup {\epsilon}\): \(\epsilon\) 也能作为状态转换的输入
- \(\sigma:~Q\times (\Sigma \cup {\epsilon}) \vdash 2^Q\)
- 第二个参数的定义域多了 \(\epsilon\)
- \(2^Q\) 就是 \(P(Q)\), 是 Q 的幂集,表示最后的状态不再是确定的一个元素,而是多个可能的状态组成的集合
-
\(\epsilon ~closure\): \(\epsilon\) -closure (q) returns all states q can reach via \(\epsilon\)-transitions, including q itself
NFA 转换方程的扩展形式 #
$$ \sigma:~Q\times\Sigma^*\vdash2^Q $$
- \(q’\) 能被扩展形式的转换方程 \(\sigma^*(q, w)\) 接受,当且仅当:
- \(q\) 经过 w 的输入到达q''
- \(q’\) 是 \(\epsilon\) -closure (q) 中的元素。
用 NFA 定义语言 #
能够被某个 NFA \(M = (Q, \sum \cup {\epsilon}, \theta, q_0, F)\) 接受的 language 记作 $$ L(M) = {w \in \Sigma^* | \sigma^*(q_0, w) \cap F \neq \varnothing} $$ 也就是说,只要最终能到的所有状态中包含最终状态,就能算作被 NFA 接受。
DFA = NFA #
- DFA只是一个特殊形式的NFA
- NFA 可以用特定算法转换成 DFA,转换前后的 language 是等价的。
子集构造法:from NFA to DFA #
- DFA 的初始状态:DFA 的初始状态进行 \(\epsilon\) 闭包计算后得到的状态集合作为 DFA 的初始状态。
- 从初始状态开始,对NFA的每个状态进行:
- 找出其对某个输入(say a)的所有转移后的状态;
- 对这些状态再进行闭包运算,得到的所有状态构成一个集合,这个集合就是 DFA 经过输入 a 后转移到的状态。
- 继续找其他的输入(当然不包括 \(\epsilon\))得到 DFA 的其他状态转移情况。
- 最后得到 DFA。
- 符号化说明:
-
- 🌰:
-
在子集构造法中,DFA的每个状态都是NFA状态的集合。因此,如果NFA有n个状态,那么DFA的状态数量最多可以是 \(2^n\) 个,因为n个状态的所有可能子集数量是 \(2^n\)。
对于每一个n,都存在一些n-状态的NFA,其中从初始状态集合出发,可以到达所有可能的状态子集。这意味着在最坏情况下,转换后的DFA将恰好有\(2^n\)个状态。
由于在最坏情况下DFA的状态数量是\(2^n\),因此转换过程的时间复杂度是\(Θ(2^n)\)。这表示转换过程的时间随着NFA状态数量的增加而指数增长。
当将NFA转换为DFA时,没有保证转换后的DFA会比NFA更小。实际上,由于DFA状态是NFA状态的集合,因此在最坏情况下,DFA的状态数量会远大于NFA。
Reply by Email



