Chapter 3-2 Lexical Analysis

笔记-编译原理 - 这篇文章属于一个选集。

§ 3: 本文

PART I: Regular Language
#

定义
#

如果一个语言 $L$ 能有一个 DFA/NFA $M$ ，使得 $L = L(M)$，则 $L$ 是 regular language

封闭性 Closure Properties
#

两个 regular language，他们的并、交、非、连接、逆、kleene star 也是 regular 的。 Regular language is closed under union, intersection, Reversal, complement, concatenation, and Kleene star

$L_1 \cup L2$
#

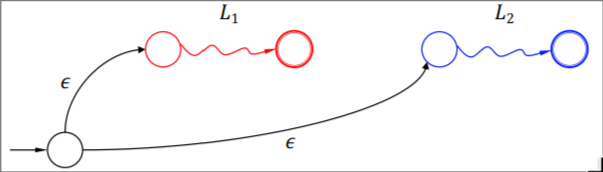
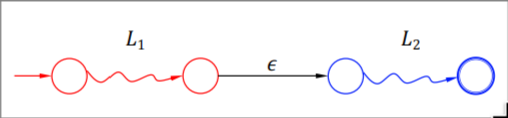
$L_1L_2$
#

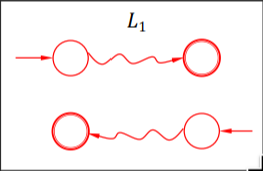
$L_1^R$
#

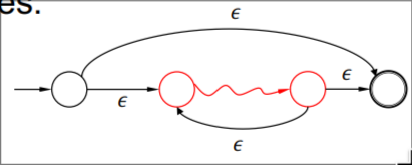
$L_1^*$
#

$\overline{L_1}$
#

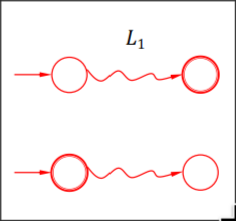
$L_1 \cap L_2$
#

好像瞪不出来了？ 🤓👆事实上，可以用前面的形式拼接而成，因为德摩根定律： $$ L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}} $$

PART II: Regular Expression (regex)
#

Regex definition
#

Regex 被递归地定义，以下的称为 regex：

Primitive regex
1. 空集（∅）：表示空语言，即不包含任何字符串
2. 空字符串（ε）：表示只包含空字符串的语言
3. 单个字符：a ∈ Σ，表示只包含字符 a 的语言
扩展法则：给定的两个 regex, 它们的：
1. 并集（Union）：如果 R 和 S 是 regex，则 R | S 也是 regex
2. 连接（Concatenation）：如果 R 和 S 是 regex，则 RS 也是 regex
3. 闭包（Kleene Star）：如果 R 是 regex，则 $R^*$ 也是 regex
4. R 是 regex, (R) 也是 regex 例如：

a*：表示所有由字符 a 组成的字符串，包括空字符串。
a|b：表示只包含字符 a 或字符 b 的字符串。
(ab)*：表示所有由 ab 重复零次或多次组成的字符串。

Language defined by regex
#

$L (\varnothing) = \varnothing;~ L (\epsilon) = {\epsilon};~ L (a) = {a}$
扩展：
1. $L (r_1|r_2) = L (r_1) \cup L(r_2)$
2. $L (r_1r_2) = L (r_1) L(r_2)$
3. $L (r_1^) = (L (r_1))^$
4. $L ((r_1)) = L (r_1)$

判断正则表达式等价
#

Two regex are equivalent if they represent the same language 也就是说分别话这两个 regex 代表的 language 对应的状态机，判断等价即可。

Laws of regex
#

和离散数学中的许多概念相似（虽然你离散数学没做笔记），regex 具有：

交换性 commutativity & 结合性 associativity
元 Identity 和零化子 Annihilator
分配律 distributive 和自反 idempotent
封闭性 Closure

Regex 与 regular language 等价
#

1. Regex->reg lang
#

Any regex represents a regular language.

回忆 regular language 的定义，发现上面的话可以等价成

任何正则表达式 (regex) 都可以对应一个 NFA/DFA.

转化方法
#

Primitive regex 可以用 NFA/DFA 表示：
Regex 的扩展法则也能用 NFA/DFA 表示，怎么证明？
- 回忆我们之前是如何通过拼接构造新的自动机来证明 reg Lang 在并、连接、kleene star 下是封闭的。这分别对应 regex 的三个（其实有四个，只不过最后一个是废话）扩展法则。
总结
1. 把目标 regex 用语言表示且化成最简形式；
2. 把最小单元的 primitive regex 的状态机画出来;
3. 根据语言的并/连接/star, 把这些基础的状态机拼接起来
例子

2. Reg Lang->regex
#

Any regular language can be expressed by a regex.

和前面的套路一样，可以理解成

任何一个 DFA 都可以被一个 regex 表示。

转化方法
#

把每个状态用距离小于等于一的状态表示
化简

PART III: Lexical Analysis
#

词法分析究竟如何工作？

为词素（如数字、变量等）编写正则表达式；
基于 regex, 构建 NFA->化简成 DFA 如果一开始不是 DFA->将 DFA 最简化
将源代码视作一个长长的输入字符串
将输入字符串与构建好的 DFA 匹配，细节上让多个 DFA 共同工作，需要的特性有
1. DFA 有不同的优先级，先匹配… 再匹配… 这样
2. 贪婪匹配，总是匹配符合正则表达式的最长字符串

PART IV: Pumping Lemma
#

泵引理。

假设存在一个 regex, 对应的状态机称作 $M$，对应的语言称作 $L$。如果一个字符串 $w \in L$, 并且 $w$ 足够长——具体来说，如果 $w$ 长到 $|w| \geq m$，其中 m 是状态机的状态总数，那么 w 输入状态机所走过的路径中必定含有重复路径，也就是走过了不止一次的路径。

这个重复的路径就是"泵"，容易知道可以在 $w$ 的基础上构造字符串，字符串中这个“泵”可以重复无数次，重复后得到的字符串一定还是在这个正则表达式对应的语言中（因为还是可以被状态机 $M$ 所接受）。

严格定义
#

如果

$L$ 是一个无限的正则表达式，则
一定存在一个正整数 $m$,
对任何 $w \in L$ 并且 $|w| \geq m$ 的字符串 $w$，
我们都能把 $w$ 写成 $$w=xyz$$ 其中 $|xy| \leq m$ 且 $|y| \geq 1$, 使得 $$w_i=xy^iz \in L$$ 其中 $i \geq 1$.

这个定义中 y 就是可以不同重复的泵，只要找到的特殊字符串足够长，就可以认为这个 y 存在。

有什么用？
#

可以用该引理的逆否命题来证明一个字符串/语言并非 regular:

对于任何一个正整数 $m$,
如果存在 $w \in L$ 使得 $|w| \geq m$
自行挑一组 $xyz$，使得 $w = xyz, y \neq \epsilon, |xy| \leq m$
如果还能找到一个 k, 使得 $xy^kz \notin L$
那么就能证明 $L$ 并非正则！

例证
#

例如，考虑语言 $L = {a^n b^n | n ≥ 0}$，即由相同数量的 $a$ 和 $b$ 组成的字符串。假设这个语言是正则的，那么根据泵引理，存在一个泵长度 $p$。选择一个字符串 $w = a^p b^p$，它显然属于 $L$。根据泵引理，$w$ 可以分解为 $w = xyz$，其中 $|xy| ≤ p$，$|y| ≥ 1$。因为 $w$ 的前 $p$ 个字符都是 $a$，所以 $y$ 必然只包含 $a$。假设 $y = a^k$，其中 $k ≥ 1$。

现在，考虑字符串 $xy^2z = a^{(p+k)} b^p$。这个字符串显然不属于 $L$，因为它包含的 $a$ 的数量多于 $b$ 的数量；但是根据泵引理他又应该是属于 $L$ 的。因此语言 $L$ 不是正则的。

Reply by Email